Sorun O (polilog (b)) içinde çözülebilir.
f(d, n)Basamak toplamı n'ye eşit veya daha küçük olan d'ye kadar ondalık basamağın tam sayıları olarak tanımlarız . Bu fonksiyonun formül tarafından verildiği görülebilir.

Daha basit bir şeyle başlayarak bu işlevi elde edelim.
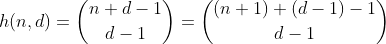
H işlevi, n + 1 farklı öğe içeren bir çoklu kümeden d - 1 öğelerini seçme yollarını sayar. Aynı zamanda n'yi d bölmelerine ayırmanın, n etrafına d - 1 çitler inşa ederek ve her ayrılmış bölümü toplayarak kolayca görülebilen yolların sayısıdır. N = 2, d = 3 'için örnek:
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Bu nedenle, h, n ve d basamaklarının basamak toplamına sahip tüm sayıları sayar. Sadece rakamlar 0 - 9 ile sınırlı olduğu için sadece 10'dan az n için çalışır. Bunu 10 - 19 değerleri için düzeltmek için, bundan sonra taşan çöp kutuları çağıracağım, 9'dan büyük bir sayıya sahip bir bölmeye sahip bölümlerin sayısını çıkarmamız gerekir.
Bu terim h'nin aşağıdaki şekilde yeniden kullanılmasıyla hesaplanabilir. N - 10'u bölümleme yollarını sayıyoruz ve sonra 10'u koymak için kutulardan birini seçiyoruz, bu da bir taşan bölmeye sahip bölümlerin sayısıyla sonuçlanıyor. Sonuç aşağıdaki ön işlevdir.
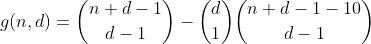
N-20'yi bölümlendirmenin tüm yollarını sayarak, daha sonra 10'ları yerleştirdiğimiz 2 bölmeyi seçerek, böylece 2 taşan bölmeyi içeren bölme sayısını sayarak, n veya daha az 29 için bu şekilde devam ediyoruz.
Ancak bu noktada dikkatli olmalıyız, çünkü önceki dönemde 2 taşmış bölmeye sahip bölümleri zaten saymıştık. Sadece bu da değil, aslında iki kere saydık. Bir örnek kullanalım ve toplamı 21 olan bölüme (10,0,11) bakalım. Önceki dönemde, 10'u çıkardık, kalan 11'in tüm bölümlerini hesapladık ve 10'u 3 seleden birine koyduk. Ancak bu bölüme iki yoldan biriyle ulaşılabilir:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Bu bölümleri de ilk dönemde bir kez saydığımızdan, 2 taşan kutulu toplam bölüm sayısı 1 - 2 = -1'dir, bu nedenle bir sonraki terimi ekleyerek bir kez daha saymamız gerekir.
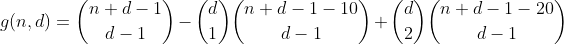
Bunu biraz daha düşünerek, belirli bir terimde belirli sayıda taşan bölmeye sahip bir bölümün sayılma sayısının aşağıdaki tablo ile ifade edilebileceğini keşfediyoruz (sütun i terimi i, j taşma ile satır j bölümlerini temsil eder) depo).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Evet, Paskal üçgeni. İlgilendiğimiz tek sayı ilk satırdaki / sütundaki sayımdır, yani sıfır taşmış bölmelere sahip bölüm sayısı. Ve her satırın, ancak ilk satırın alternatif toplamı 0'a eşit olduğu için (örneğin, 1 - 4 + 6 - 4 + 1 = 0), onlardan nasıl kurtuluruz ve sondan önceki formüle ulaşırız.
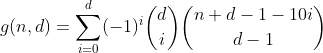
Bu işlev, n basamaklı toplamına sahip d basamaklı tüm sayıları sayar.
Şimdi, rakam toplamı n'den küçük olan rakamlar ne olacak? Binomlar için standart bir tekrarlama artı bir endüktif argüman kullanabiliriz.
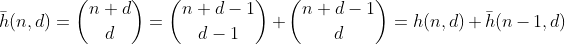
en fazla hane toplamı olan bölüm sayısını sayar. Ve bundan f, g ile aynı argümanlar kullanılarak türetilebilir.
Bu formülü kullanarak, örneğin 8000 ila 8999 arasındaki ağır sayıların sayısını bulabiliriz 1000 - f(3, 20), çünkü bu aralıkta bin sayı vardır ve rakam toplamı 28'den küçük veya eşit olan sayıları çıkarmamız gerekir ilk rakamın rakam toplamına zaten 8 katkıda bulunduğu dikkate alınır.
Daha karmaşık bir örnek olarak, 1234..5678 aralığında ağır sayıların sayısına bakalım. Önce 1234'ten 1240'a 1'lik adımlarla gidebiliriz. Sonra 1240'dan 1300'e 10'luk adımlarla gidebiliriz. Yukarıdaki formül bize bu aralıklardaki ağır sayıların sayısını verir:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Şimdi 100 adımda 1300'den 2000'e gidiyoruz:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
2000'den 5000'e 1000'lik adımlarla:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Şimdi adım boyutunu tekrar, 100'lük adımlarda 5000'den 5600'e, 10'lu adımlarda 5600'den 5670'e ve son olarak 1'lik adımlarda 5670'den 5678'e düşürmeliyiz.
Örnek bir Python uygulaması (bu arada hafif optimizasyonlar ve testler aldı):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Düzenleme : Kodu optimize edilmiş bir sürümle değiştirildi (orijinal koddan daha çirkin görünüyor). Ben varken de birkaç köşe durumlarda düzeltildi. heavy(1234, 100000000)makinemde yaklaşık bir milisaniye sürüyor.
