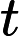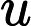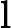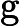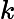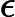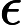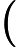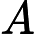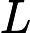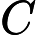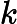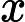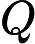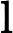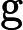NP orta statüsü için neden bu kadar az doğal aday var?

Ladner Teoremi tarafından iyi bilinir, eğer , o zaman sonsuz sayıda N P- orta ( N P I ) problemi vardır. Bu durum için Graph Isomorphism ve diğerleri gibi doğal adaylar da var, bakınız P ve NPC Arasındaki Sorunlar . Bununla birlikte, bilinen taraftar büyük çoğunluğu , n , bir t u r bir l N P -Sorunları ya olduğu bilinmektedir P veya N P C . Bunların sadece küçük bir kısmı N P I için aday olmaya devam ediyor${\mathsf P}\neq \mathsf {NP}$$\mathsf {NP}$$\mathsf{NPI}$$natural$ $\mathsf {NP}$$\mathsf {P}$$\mathsf {NPC}$$\mathsf {NPI}$. Başka bir deyişle, bilinenler arasında rastgele bir doğal sorunu seçersek, bir N P I adayı seçme şansımız çok az . Bu fenomen için herhangi bir açıklama var mı?$\mathsf {NP}$$\mathsf {NPI}$

Felsefi açıdan, 3 olası açıklama düşünebilirim:

1. Bu kadar küçük bir doğal adayının küçük bir kısmına sahip olmanın nedeni , sonunda N P I'in boş olacağıdır. Biliyorum, bu P = N P anlamına geliyor, bu yüzden pek mümkün değil. Bununla birlikte, bir kişi hala (onlardan biri olmasam da) doğal N P I problemlerinin nadirliğinin, diğer pek çok gözlemin aksine P = N P'yi desteklediği görünen ampirik bir gözlem olduğunu iddia edebilir .$\mathsf {NPI}$$\mathsf {NPI}$${\mathsf P} =\mathsf {NP}$$\mathsf {NPI}$${\mathsf P} =\mathsf {NP}$

2. "Natural " nin küçüklüğü, kolay ve zor problemler arasında bir tür keskin faz geçişini temsil eder. Anlaşılan, anlamlı, doğal algoritmik problemler kolay ya da zor olma eğilimindeymiş gibi davranırlar, geçiş dardır (ancak hala mevcuttur).$\mathsf {NPI}$

3. Sonunda "doğal- tüm sorunlar: 2'de argüman aşırı alınabilir " içine konacak P ∪ N P C , henüz P ≠ N P , böylece N P ı ≠ ∅ . Bu, N P I’de kalan tüm problemlerin olduğu anlamına gelir.$\mathsf {NPI}$$\mathsf {P} \cup \mathsf {NPC}$${\mathsf P}\neq \mathsf {NP}$$\mathsf {NPI}\neq \emptyset$$\mathsf {NPI}$"doğal" dır (gerçek hayat anlamı olmadan). Bunun yorumlanması, doğal sorunların ya kolay ya da zor olduğu olabilir; geçiş, "fiziksel" bir anlamı olmayan, yalnızca mantıksal bir yapıdır. Bu, bir şekilde mantıklı olan, ancak herhangi bir fiziksel niceliğin ölçülen değeri olarak ortaya çıkmayan irrasyonel rakamlar durumunu hatırlatıyor. Dolayısıyla, fiziksel gerçeklikten gelmezler, daha çok o gerçekliğin "mantıksal kapanışı" içindedirler.

En çok hangi açıklamayı seviyorsunuz veya başka bir tanesini önerebilir misiniz?

Diğerlerinin de belirttiği gibi, açıklamaya çalıştığınız şeyin ne kadar doğru olduğu tartışmalıdır. Bir tanesi, 60'lı ve 70'li yıllarda teorik bilgisayar bilim adamlarının, P ya da NP-tamamında ortaya çıkan problemlerle daha fazla ilgilendiklerini iddia edebilirler. Günümüzde, karmaşıklık-teorik şifreleme, kuantum hesaplama, kafes vb. Yükselişinden dolayı - ve NP'nin bütünlüğünün çok iyi anlaşıldığı basit bir gerçek - --- gittikçe daha fazla ilgilenmeye başladık. NP-orta olduğu ortaya çıkan sorun türleri.

Yine de, şunu sorabilir: bir şeyin doğru olduğu ölçüde - yani, pek çok doğal arama ve optimizasyon probleminin ya NP-tam ya da P'de başka bir şeyle - "o kadar" "başa çıkma" derecesi. , neden doğru? Burada, hesaplanabilirlikten daha önceki bir fenomene bakarak çok fazla sezgiye sahip olabileceğinizi düşünüyorum: bu kadar doğal hesaplama modelinin Turing-eksiksiz olmak için "takıldığını". Bu durumda, sana vb birkaç temel bileşenleri --- okuma / yazma belleği, döngüler, conditionals, bir kez .--- o zor açıklama, yani söyleyebilirim kaçınmakbir Turing makinesini taklit edebilme ve bu nedenle Turing tamamlandı. Aynı şekilde, arama veya optimizasyon probleminiz birkaç temel bileşene sahip olduktan sonra - en önemlisi, VE, VEYA gibi mantık kapılarını taklit eden "gadget'lar" oluşturma yeteneği - mümkün olmamak SAT kodlamak ve bu nedenle NP tamamlamak.

Düşünmeyi sevdiğim gibi, SAT gibi problemler çevrelerindeki diğer tüm hesaplama problemlerinde güçlü bir "yerçekimsel çekiş" yaratıyor, bu da NP-tamamlanmalarını "engellemek" istiyor. Bu yüzden, normalde, başka bir problem o çekişe ulaştığında bile özel bir açıklama gerektirmez! Bir (görünüşte) sert NP problem sağlayan bazı mülk sahip olduğunda daha çarpıcı ve daha açıklama ihtiyacı olan şey, karşı SAT çekim gücünü. Sonra bilmek istiyorum: Ne olduğunu bu özellik? Neden sen kodlamak Boole mantık kapıları o aygıtları inşa etmenin, bu sorun için olağan NP-tamlık hile çalamaz? Bu son CS.SE cevabında bu sorunun bazı ortak cevaplarının bir listesini yaptım., ama (başka bir yorumcunun daha önce işaret ettiği gibi) kaçırdığım başka olası cevaplar da var.

Birçok doğal problem Kısıt Memnuniyet Problemleri olarak ifade edilebilir ve CSP'ler için ikilik teoremleri vardır.

Sadece bir şaka: Scott Aaronson'un güzel cevabındaki "SAT yerçekimi çekme" yi düşündükten sonra aklıma başka bir metafor geldi: 3-SAT 2-SAT sandviçi !

... ama sandviçin doğal malzemelerle dolup dolmadığını bilmiyorum (bununla birlikte biraz doluydu -SAT sosu [1] Üstel-Zamanlı Hipotez doğruysa) :-D$(2 + \frac{(\log n)^k}{n^2})$

[1] 'deki bir diğer sonuç ile doldurulmamasıdır .$(2+1/n^{2−\epsilon}),0<\epsilon<2$

[1] Yunlei Zhao, Xiaotie Deng, CH Lee, Hong Zhu, -SAT ve özellikleri$(2+f(n))$ , Ayrık Uygulamalı Matematik, Cilt 136, Sayı 1, 30 Ocak 2004, Sayfa 3-11, ISSN 0166 -218X.

Çok fazla sayıda doğal orta sorun olması ihtimalini ortadan kaldıramıyoruz . Belirgin kıtlığı nedeniyle kanıtlamak için gerekli olan teknik ve araçların eksikliği olan K P bazı olası karmaşıklığı varsayım (Arora ve Barak ispat değildir belirtilmelidir altında Ara tepkime durumu N P herhangi bir doğal Ara tepkime durumu K P da varsayarak sorun P ≠ N P ).$NP$$NP$$NP$$NP$$P \ne NP$

Doğal orta sorunların taşkınlarının açık olduğu anlaşılmaktadır . Jonsson, Lagerkvist ve Nordh, Ladner'in sorunlara üfleme delikleri olarak bilinen köşegenleştirme tekniğini genişletti ve bunu Kısıt Memnuniyeti Sorunları'na uyguladı. N P- orta durumu için aday olan bir CSP aldı . Önerme kaçırma sorununun N P- orta parçalara sahip olduğunu kanıtladılar .$NP$$NP$$NP$

$NP$$FPT \ne W[1]$

Kaynaklar :

1- M. Grohe. Homomorfizmin karmaşıklığı ve diğer taraftan görülen kısıtlama tatmini sorunları. ACM Dergisi, 54 (1), makale 1, 2007

2- Peter Jonsson, Victor Lagerkvist ve Gustav Nordh. Memnuniyeti Kısıtlayan Uygulamalar ile Hesaplamalı Problemlerin Çeşitli Yönlerinde Delikleri Açma. 19. Uluslararası Sınırlama Programlama İlkeleri ve Uygulaması Konferansı Bildirilerinde (CP-2013). 2013.

Burada NP-ara sorunların Goldilocks yapısı hakkında bir peri masalı. (Uyarı: Bu hikaye, potansiyel hipotezler üretmek ve test etmek için yararlı bir yanlışlık olabilir, ancak bilimsel olarak titiz olmak anlamına gelmez. Bir parça Kolmogorov karmaşıklık büyüsünün bir çizgisi olan Üstelik SAT teorisinden ödünç alınan Exponential Time Hipotezi'ne dayanır. çözme ve Terence Tao'nun problemler için sezgisel üçleme yöntemi, matematikle ilgili tüm el sallama çağrışımlarında olduğu gibi, kendi riski altında tüketin.

NP'deki bir problemin neredeyse tüm örnekleri yüksek düzeyde yapılandırılmışsa, sorun aslında P'dedir. Bu nedenle, hemen hemen hepsi çok fazla fazlalık içerir ve sorun için bir polinom-zaman algoritması da fazlalığı hesaba katmanın bir yoludur. EXP'deki bir problemi alıp bir miktar dolgu formu (her zamanki türden olmak zorunda değildir) kullanarak bir miktar fazlalık ekleyerek P'deki her problemin elde edilebileceği düşünülebilir. Eğer öyleyse, o zaman polinom-zaman algoritması bu dolguyu geri almak için etkili bir yol olarak görülebilir.

Yapılandırılmamış, bir "sertlik çekirdeği" oluşturan yeterli sayıda örnek varsa, sorun NP tamamlanmış demektir.

Bununla birlikte, eğer bu "sertlik çekirdeği" çok seyrekse, o zaman sadece SAT'ın bir kısmını temsil etmek için yer vardır, bu yüzden sorun P ya da NP-orta düzeydedir. (Bu argüman Ladner'ın teoreminin özüdür). Scott'ın analojisini kullanmak için, "sertliğin çekirdeği", NP-tamamlanma yönüne doğru, soruna yerçekimsel bir çekim uygular. "Sertliğin çekirdeğindeki" örnekler fazla fazlalık içermez ve tüm bu durumlar için çalışan tek gerçekçi algoritma kaba kuvvet aramadır (elbette, eğer sadece çok sayıda varsa, o zaman tablo arama da çalışır).

Bu açıdan bakıldığında, NP-ara sorunlar, uygulamada nadir olmalıdır, çünkü yapılandırılmış ve yapılandırılmamış örnekler arasında iyi bir Goldilocks dengesi gerektirir. Örnekler, bir algoritmaya kısmen uygun olmaları için yeterince fazlalığa sahip olmalı, ancak sorunun P'de olmadığı kadar sert bir çekirdek olmalıdır.

Kişi, bulmacalara dayanan daha basit (ve eğlenceli, ama aynı zamanda potansiyel olarak daha da yanıltıcı) bir hikaye anlatabilir. Sadece birkaç kısıtlama ile, bir çok arama yapılması zorlanabilir, örneğin NxN Sudoku NP tamamlandı. Şimdi tek seferde birçok küçük bulmacayı tek seferde çözmenin istendiğini düşünün (örneğin birçok 9x9 Sudokus). Alınan zaman, her bir durumdaki bulmaca sayısında kabaca lineer olacak ve bu sorun daha sonra P'de. Orta sorunlar için, bir kişi her birinin bir büyükçe (ama çok büyük değil) büyükçe üzerindeki Sudokus sayısı olduğunu düşünebilir. (ama çok büyük değil) ızgaralar. Bu tür birçok sorunu gözlemlemememizin nedeni, poz vermek ve çözmek için sıkıcı olmalarıdır!

$\mathsf{NPI}$$\mathsf{NPI}$$\mathsf{NP}$

$n$$\geq \log n$$\mathsf{NPI}$ $\mathsf{NP}$$x$$Q$$x$$Q$$\mathsf{NPI}$$\mathsf{P}$

$\mathsf{NPI}$$\mathsf{NP}$$\mathsf{NPI}$$\mathsf{NPC}$

$\mathsf{NPI}$$\mathsf{P}$