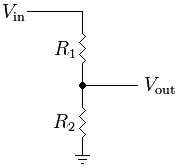
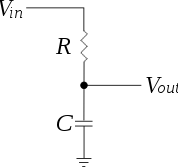
"Empedans nedir" sorusuna, empedansın genel olarak elektriksel empedansın sadece bir örnek olduğu geniş bir fizik kavramı olduğunu not edeceğim.
Ne anlama geldiğini ve nasıl çalıştığını anlamak için, bunun yerine mekanik empedansı düşünmek daha kolaydır. Zeminden ağır bir kanepeyi itmeye (kaydırmaya) çalışmayı düşünün.
Belli bir kuvvet uygularsınız ve kanepe ne kadar zorladığınıza, koltuğun ağırlığına, zemin yüzeyinin tipine, koltuğun sahip olduğu ayak tipine ve benzeri şeylere bağlı olarak belli bir hızla kayar. Bu durumda, ne kadar zor bastığınız ve kanepenin ne kadar hızlı gittiği arasındaki oranı veren bir mekanik empedans tanımlamak mümkündür.
Bu aslında bir elektrik devresine çok benzer, burada bir devre boyunca belirli miktarda voltaj uygularsınız ve akım bunun içinden belirli bir oranda akar.
Hem kanepenin hem de devrenin durumu için, girişinize verilen yanıt basit ve oldukça doğrusal olabilir: Ohm Yasasına uyan bir direnç, elektriksel empedansının yalnızca direnç olduğu ve kanepenin, buna izin veren sürtünme kaydırıcı ayaklarına sahip olabileceği bir direnç gücünüzle orantılı bir hızla hareket etmek. *
Devreler ve mekanik sistemler de doğrusal olmayabilir. Devreniz bir diyotla seri halinde bir direnç boyunca yerleştirilmiş değişken bir voltajdan oluşuyorsa, akım, Ohm'a uygun olarak direnç boyunca akmaya başlayacağınız diyotun ileri voltajını geçene kadar sıfıra yakın olacaktır. yasa. Aynı şekilde, yerde oturan bir koltukta genellikle bir dereceye kadar statik sürtünme olacaktır: belli bir miktarda ilk kuvvetle itene kadar hareket etmeye başlamaz. Ne mekanik ne de elektrik sistemde tanımlanabilecek tek bir doğrusal empedans yoktur. Aksine, yapabileceğiniz en iyisi, farklı koşullar altında empedansları ayrı ayrı tanımlamaktır. (Gerçek dünya bundan daha fazlasıdır.)
Her şey çok net ve doğrusal olsa bile, empedansın sadece bir oranı tanımladığını belirtmek önemlidir - sistemin sınırlarını tanımlamaz ve "kötü" değildir. Kesinlikle daha fazla gerilim / zorlama ekleyerek (ideal bir sistemde) istediğiniz kadar akım / hız elde edebilirsiniz.
Mekanik sistemler de ac empedansı için oldukça iyi bir his verebilir. Bisiklete bindiğinizi hayal edin. Pedalların her yarım çevrimi sırasında sola, sağa itin. Pedalınızın her döngüsünde itip çekeceğiniz şekilde sadece bir ayak ve bir ayak klipsi ile pedal çevirmeyi de hayal edebilirsiniz. Bu, bir devreye bir ac voltajı uygulamak gibi bir şey: belirli bir frekansta, sırayla, bastırıp çekiyorsunuz.
Frekans yeterince yavaşsa - bisiklete bindiğinizde olduğu gibi, pedalları aşağıya itme problemi, kanepeyi itmek gibi sadece "dc" bir problemdir. Hızlandığınızda, işler farklı şekilde hareket edebilir.
Şimdi, belli bir hızla bisiklet sürdüğünüzü ve bisikletinizin düşük, orta ve yüksek vites oranları ile üç hızlı olduğunu varsayalım. Orta, doğal hisseder, yüksek vites, herhangi bir fark yaratmak için yeterli güç uygulamak zordur ve düşük viteste, pedallara enerji aktarmadan sadece pedalları döndürürsünüz. Bu, ayağa bir miktar fiziksel direnç gösterdiklerinde, tekerleklere yalnızca etkili bir şekilde güç aktarabileceğiniz - çok fazla değil, çok az olmayan - bir empedans uyumu meselesidir . Karşılık gelen elektriksel fenomen de çok yaygındır; RF gücünü etkili bir şekilde A noktasından B noktasına iletmek için empedans uyumlu hatlara ihtiyacınız vardır ve iki iletim hattını birbirine bağladığınızda arayüzde bir miktar kayıp olur.
Pedalların ayağınıza sağladığı direnç, ne kadar zor bastığınızla orantılıdır; bu da en düşük hızda, basit bir dirençle en yakından ilişkilidir. AC devrelerinde bile, bir direnç bir direnç gibi davranır (belirli bir noktaya kadar).
Bununla birlikte, bir dirençten farklı olarak, bir bisikletin empedansı frekansa bağlıdır. Bisikletinizi durmadan başlayarak yüksek vitese aldığınızı varsayalım. Başlamak çok zor olabilir . Ancak, bir kere başladığınızda, pedalların sunduğu empedans daha hızlı giderken aşağı iner ve çok hızlı gittikten sonra, pedalların ayaklarınızdaki gücü emmek için çok az empedans sunduğunu görebilirsiniz. Bu yüzden aslında yüksek başlayan ve daha yüksek frekansa yöneldiğiniz zaman azalan frekans bağımlı bir empedans (bir reaktans ) var.
Bu, bir kondansatörün davranışına çok benzer ve bir bisikletin mekanik empedansı için oldukça iyi bir model, bir kondansatöre paralel bir direnç olacaktır.
DC'de (sıfır hız), empedansınız olarak sadece yüksek, sabit direnci görürsünüz. Pedal çevirme frekansı arttıkça, kapasitör empedansı direncinkinden daha düşük hale gelir ve akımın bu şekilde akmasına izin verir.
Elbette, çeşitli diğer elektrikli bileşenler ve bunların mekanik analojileri vardır **, ancak bu tartışma, zaman zaman neyin göründüğünün matematiksel yönlerini öğrenirken, genel kavram hakkında topraklanmış kalmaya yönelik (başlangıçta düşünülen) bazı ilk sezgileri vermelidir. çok soyut bir konu gibi.
* Seçiciye bir kelime: Ohm kanunu hiçbir zaman gerçek bir cihaz için kesin değildir ve gerçek dünya sürtünme kuvvetleri hiçbir zaman kuvvetle tam olarak orantılı olarak hız vermez. Ancak, "oldukça doğrusal" kolaydır. Burada tüm eğitimsel şeyler olmaya çalışıyorum. Bana biraz gevşeyin.
** Örneğin, bir indüktör, daha yüksek frekansa ulaşırken sürükleme ekleyen tekerlekinizde yay yüklü bir silindir gibidir.)