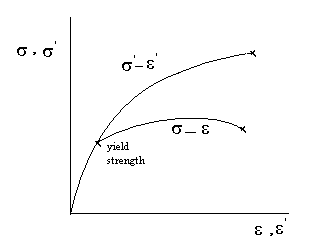Neden mühendislik stresi kullanıyoruz?

Şaşırtıcı bir şekilde bu daha önce sorulmadı, bu yüzden basit bir şey eksik olmalı.

Bu denklemde mühendislik stresi ve mühendislik zorlaması kullanıyoruz. Stres = (Young modülü) × (zorlanma). Bu ek. bükme kirişleri, büküm şaftları ve burkulma analizlerinde kullanılır. Bükme son denklem yüzden ve burulma verecek bize mühendislik stresinin değeri ama stresin değeri değil.$(\frac{M}{I} = \frac{\sigma}{y})$$(\frac{T}{I} = \frac{\tau}{r})$

Doğru stres değerini vermeyeceğini bildiğimiz halde neden gerçek stres yerine mühendislik stresi düşünüyoruz?

Okuduğum bazı şeyler:

1. Ölçülmesi zor.
2. Çok fazla bir fark yok ve sadece bir Güvenlik Faktörü uygulayabiliriz.
3. "Yüklemeden sonra malzemelerin kesit alanlarını değiştireceğini düşünmüyoruz, çünkü plastik bölge deformasyonu olmayacak şekilde tasarlıyoruz.

Birincisi, 1 ve 2 benim için gerçek nedenler değil. 3 numara her zaman elastik bölgede tasarladığımız için makul görünüyor, ama bu öyle mi? Mühendislik zorlaması oransal sınırdan sonra bile geçerli bilgi veriyor mu?

Mühendislik gerginliğini "doğru" değer olmasa da kullanıyoruz, çünkü çoğu durumda, özellikle elastik rejimde, mühendislik gerginliği gerçek gerginlikten ihmal edilebilir derecede farklıdır.

Lineer elastik, Hookean malzemeler için, genellikle elastik sınırdaki durum zorlaması çok küçüktür. Örneğin, en güçlü çeliklerin bile, soğuk yaklaşık bir üst sınır vardır . Çelik modülü yaklaşık olarak . Böylece en güçlü çelikler için . Yani plastik deformasyonun başlangıcında, mühendislik zorlanması . Birçok kullanışlı elastik malzeme, elastik sınırlarında çok daha düşük mühendislik gerginliğine sahiptir. e = 200 x 10 9 Pa ε El = 0.005 = 0.5 ,% 0.5 $\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$$E=200\times 10^{9}\ \textrm{Pa}$$\varepsilon_{\textrm{el}}=0.005=0.5\%$$0.5\%$

İzotropik, Hookean elastik katı için aşağıdakiler doğrudur

$$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$$

seçiminde genel kayıp olmadan . Elastik tek eksenli gerginlikte , malzemenin büzülme serbest olduğu varsayılarak . Böylece . Elastik rejimdeki çelikler için Poisson oranı yaklaşık 0,3 olduğundan, enine kesitsel doğrusal basınç suşu . Elastik enine kesit alanı ya da orijinal alanın katına çok yakındır . σ x 2 = σ x 3 = 0 ε x 2 = ε x 3 = - σ el$x_{i}$$\sigma_{x_{2}}=\sigma_{x_{3}}=0$ν0.0015(1-0.0015)2A0$\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$$\nu$$0.0015$$(1-0.0015)^{2}A_{0}$$0.997$

Dolayısıyla, gerçek suş, elastik mühendislik suşundan kat daha büyük veya yaklaşık kat veya yaklaşık daha büyüktür. Bunun son derece güçlü doğrusal elastik bir malzemenin elastik sınırında olduğunu ve elastik rejimdeki gerçek gerilme ile mühendislik gerilmesi arasındaki farkın makul derecede muhafazakar bir tahmin olduğunu unutmayın. 1,0030,3$\frac{1}{0.997}$$1.003$$0.3\%$

Yukarıdaki analiz doğrusal olarak elastik olan Hookean katılar için oldukça yararlı olsa da, polimerler ve biyolojik malzemeler için oldukça iyi değildir. Bu tür malzemeler genellikle viskoelastiktir (veya tamamen başka bir malzeme sınıfıdır) ve bu nedenle davranışlarında farklı kurallara uyarlar. Gerçek suş, aşağıdaki grafikte de görüldüğü gibi, plastik rejimdeki mühendislik suşundan oldukça çılgınca ayrılmaktadır ( burada bulunur )

Puanlarınız için:

1. Deformasyon sırasında enine kesit alanında değişiklik Ölçüm olan zor. Hassas şekilde işlenmiş test numuneleri üzerine kalibre edilmiş enstrümantasyonun dikkatle yerleştirilmesini gerektirir. Bir kullanabilir deformasyon ölçüm aletlerinin bir yüzüne yerleştirilen çekme çubuğu tek eksenli gerilim ve sıkıştırma altındaki yanal gerginlik ölçmek için çekme test ekipmanları . İstatistiksel olarak anlamlı sonuçlar elde etmek, önemli zaman, çaba ve maliyetin yanı sıra birçok örnek alır.

2. Orada ise az fark. Umarım yukarıdaki farkın ne kadar küçük olduğunu yeterince açıklamışımdır: Muhafazakar bir vakada yaklaşık fark hesapladım .$0.3\%$

3. Elastik rejimin sonundan başka bir şeyi görmezden gelebileceğimiz veya her zaman elastik rejim için tasarladığımız fikri doğru değildir. Plastik deformasyon genellikle çalışmaya değer olabilir. Haddeleme, çekme, ekstrüzyon vb. Gibi sürekli şekil verme süreçlerinin modellenmesi, başarılı bir performans için plastik deformasyon mekaniğinin derinlemesine anlaşılmasını gerektirir ve bu amaçla gerçek stres ve gerçek gerginlik paha biçilmezdir. Özellikle tel çekme için bakınız (bu pdf ) ve denklem 7'yi bulun. Plastik deformasyon ayrıca bir çarpışma sırasında araç gövdesi panelleri ve çerçeve bileşenleri gibi bazı beklenen kullanım durumlarında kalıcı olarak deforme olması gereken malzemelerin modellenmesi için de yararlıdır. Plastik deformasyon yararlıdır çünkü kinetik enerjiyi emer.

Edit: Özür dilerim, aslında stres için soruya cevap vermedi. Bununla birlikte, elastik rejimdeki doğrusal ilişkileri göz önüne alındığında, gerilme için aynı noktaların gerilim için geçerli olduğu oldukça açık olmalıdır. Yine, plastik rejiminde büyük varyasyonlar olabilir.

@ Starrise'nin cevabına ekleniyor:

Neden 1 ve 2'nin reddedilmesi ile ilgili olarak, bunlarla ilgili maliyet-fayda analizini göz önünde bulundurmayı unutuyorsunuz. @Starrise yanıtlarında gösterdiği gibi, fark genellikle önemli değildir (diğer materyaller genellikle daha büyük farklılıklara sahip olacaktır).

$\pm6\%$ $\pm15\%$

Peki, diğer tüm özelliklerin (akma dayanımı ve kesit boyutları dahil), kullanımından dolayı "hatayı" atmaktan kesin olan rastgele dalgalanmalara sahip olması durumunda, günlük mühendislik pratiğinde gerçek zorlamayı dikkate almanın anlamı nedir? gerçek gerginlik yerine mühendislik gerginliği?