Bu, bu soruya dayanarak sormam için ilham aldığım bir soru , ki bu kuantum tavlamanın hesaplama için normal devre modelinden tamamen farklı bir model olduğunu not ediyor. Bunu daha önce duymuştum ve benim kapı modelinin kuantum tavlama için geçerli olmadığını anladım, ancak bunun neden olduğunu veya bir sertifikanın yapabileceği hesaplamaların nasıl ayrıştırılacağını tam olarak anlamadım. Birkaç görüşmeden anladığım kadarıyla (bazıları kendileri tarafından D-dalgasıyla!) Anlaşıcıların belirli bir Hamiltonian ile sınırlı olduğu gerçeği, içine giriyor.
Kuantum tavlaması neden geçit modeli ile tanımlanamıyor?
Yanıtlar:
D-Wave makinesi gibi bir Quantum Annealer, Ising modelinin fiziksel bir temsilidir ve bu nedenle H P = n ∑ J = 1 h j σ z j + ∑ i , j J formundaki bir 'problem' Hamiltoniyeni vardır. i j σ z i σ z j .
Temel olarak, çözülecek sorun yukarıdaki Hamiltonyen'le eşleştirilir. Hamilton sistem başlar ve tavlama parametresi, s ilk Hamilton eşlemek için kullanılan H I sorun Hamilton için H P kullanılarak H ( ler ) = ( 1 - s ) 'H I + s , H p .
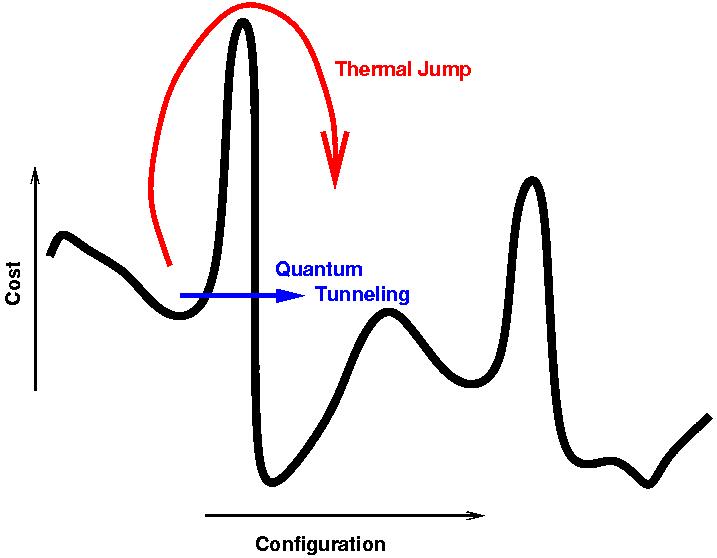
Bu bir tavlama olduğu için, işlem, sistemin temel durumuna yakın kalacak kadar yavaş bir şekilde gerçekleştirilirken, Hamiltonian, Nat'ın cevabında açıklandığı gibi temel duruma yakın kalmak için tünel kullanarak, probleminkine göre değişir .
Şimdi, neden bu bir kapı modeli QC'yi tanımlamak için kullanılamıyor? Yukarıdakiler, NP-zordur olan, Quadratic kısıtsız bir ikili optimizasyon (QUBO) problemidir ... Gerçekten de, burada, Ising modeline bir dizi NP problemini haritalayan bir makale . NP'deki herhangi bir problem polinom zamandaki herhangi bir NP zorlu problemle eşleştirilebilir ve tamsayılı çarpanlara ayırma aslında bir NP problemidir.
Bunun (prensipte) yaptığı şey, kesin sonuçlara çok hızlı bir şekilde yaklaşmak, çok hızlı bir şekilde, ancak bu, “neredeyse doğru” dan “doğru” ya gitmek için kesin sonucun gerekli olduğu hiçbir şeye yardımcı olmuyor. yani, muhtemelen hala genel olarak NP, asıl sorun NP ise) bu durumda, 'neredeyse doğru' bir çözüm olan / veren parametrelerin zorunlu olarak / verilen parametrelerin yakınında hiçbir yere dağıtılmayacağından doğru çözüm.
Açıklama için düzenleme: bunun anlamı, kuantum tavlama cihazının (QA), evrensel bir QC'nin üssel bir hızlanma sağladığı ve aynı problemi çözebildiği tam sayı çarpanlarına ayırma gibi NP sorunlarını çözmek için hala üssel zaman (potansiyel olarak daha hızlı üssel zaman) almasıdır. poli zamanında problem. Bu, bir KG'nın evrensel zamandaki bir QC'yi zaman içerisinde simüle edemediği anlamına gelir (aksi halde çoklu zaman içinde yapamadığı sorunları çözebilir). Yorumlarda da belirtildiği gibi, bu, bir KG'nin veritabanı araştırması gibi diğer sorunlarda aynı hızda olamayacağını söylemekle aynı şey değildir .
1
Eğer doğru anlarsam, temelde bir kuantum tavlayıcısının kuantum devresini tanımlayamayacağını söylüyorsunuz, çünkü keyfi bir Hamiltonian'ın minimumunu bulma sorunu NP-zor. Bu ima anlamıyorum. Kuantum devrelerini simüle etmek de genel olarak klasik olarak benzetmek zordur (bkz. Örneğin 1610.01808 )
—
glS
Ayrıca, kuantum devreleri olarak ifade edilen algoritmalar yoluyla çözülebilen bazı problemlerin, kuantum tavlama yoluyla da çözülebildiği bilinmektedir. Dikkate değer bir örnek veritabanı araştırmasıdır (bakınız örneğin 1006.1696'nın II . Bu demektir ki bu bir anlamda bir kutu , bazı durumlarda bir q tavlama sorun haline sulu devre mesafededir. Bu aynı zamanda üçüncü paragrafınızı geçersiz kılmaz mı (özellikle, bunun bir geçit modeli
—
QC'yi
@glS hayır, hiç de değil - NP zor bir sorunun min'ını (ikinci yorumunuzdaki makaleye göre) bulmak için üstel bir zaman alır, bu nedenle hızlandırmanın olabileceği P (örneğin veritabanı araması) problemleri varken evrensel QC ile eşleştirilebiliyorsa, bir NP problemini çözmek hala sınırlı bir hata dahilinde olmak için üstel bir zaman alır, burada evrensel bir QC aynı problemi poli zamanında, örneğin tamsayı çarpanlarında çözebilir. QA bunu yapamadığı için, bir QA poli zamanında evrensel bir QC'yi simüle edemez
—
Mithrandir24601
Tamam, ama cevabında söylediğin şey bu değil (ya da en azından açıkça değil). Cevaptan, QA'nın kapı modeli QC yoluyla çözülen bir sorunu çözmek için asla kullanılamayacağını söylüyor gibi görünüyorsunuz. Bu QA verimli bir NP-zor problemi (çözemez söyleyerek çok farklı olabilir biz Faktoring gerçekten olup olmadığını bilmiyorum gibi bu kanıtlanmıştır sanmıyorum gerçi ... bazen kuantum devre ile çözülecek NP-zor ve kuantum avantajının gösterilmiş olduğu diğer pek çok sorun benim bilgime göre karar sorunları değildir.
—
glS
Umarım işleri açıklığa kavuşturan bir düzenleme yaptım. P = NP olup olmadığına dair kesin bir bilgi yoktur, fakat mevcut bilgiye göre hala QC'nin katlanarak daha hızlı olduğu konusunda özel bir örnek
—
Mithrandir24601
Tavlama daha çok analog bir taktiktir.
Temel amaç, optimize etmek istediğiniz tuhaf bir işleve sahip olmanızdır. Yani, etrafında zıplarsın. İlk başta, " sıcaklık " çok yüksektir, öyle ki seçilen nokta çok fazla sıçrayabilir. Ardından algoritma " soğudukça " sıcaklık düşer ve zıplama daha az agresifleşir.
Sonuçta, ideal olarak küresel optima'ya benzeyen yerel bir optimaya yerleşir.
Simüle edilmiş tavlama için bir animasyon (kuantum olmayan):
Ancak, kuantum tavlama için hemen hemen aynı konsept :
Buna karşılık, kapı mantığı analogdan çok daha dijitaldir. Sadece kaotik zıplamadan sonra bir sonuç bulmak yerine, qubitlerle ve mantıksal işlemlerle ilgileniyor.
Teşekkürler, bu benim için bazı sınırlamaları netleştiriyor. Tavlama problemi olarak tekrar ifade etmenin mümkün olmadığı herhangi bir problem biliyor musunuz (Vikipedi'nin Shor algoritmasının mümkün olmadığını, çünkü "tepe tırmanma" problemi olduğunu biliyorum, ama bunun özellikleri hakkında daha fazla şey biliyorsanız, ben onları duymak isterim :)
—
Emily Tyhurst
@EmilyTyhurst Teknik olarak, herhangi bir sorun tepe tırmanma terimleriyle tanımlanabilir. Tepenin tırmanma biçiminde açıklandığı zaman, sorunun ne kadar iyi davranıldığına dair bir soru da var. İyi uymayan problemler inanılmaz derecede çirkin olabilir. Tamamen dışbükey olmayan sorunlar için, tepe tırmanma, en iyi ihtimalle, temel olarak kaba kuvvet arayışı olacaktır.
—
Nat
@EmilyTyhurst Hah opps, yorumunuzu ters yönde yanlış okudu. xD Ama evet, klasik bir bilgisayarda yaptığınız gibi kuantum bir bilgisayarda tavlama simülasyonu yapabilirsiniz. Sonra, buna " kuantum tavlama " diyoruz ya da olmasın , anlambilim meselesi haline gelir.
—
Nat
@EmilyTyhurst Evet, kesinlikle hepsi dönüştürülebilir. Yani, Turing eksiksizliği kavramı gibi bir şey - eğer bir tür tam mantığa sahipsek, onunla hemen hemen başka bir şey inşa edebiliriz.
—
Nat
Önemli bir kuantum tavlama noktası, Hamiltonianı adyabatik olarak değiştirerek, devletin her zaman (değişen) Hamiltonian'ın temel durumu olarak kalması ve protokolün hedefi olan nihai Hamiltonian'ın gs'si ile bitmesidir. . Bu, burada tarif ettiğiniz "atlama" ile nasıl ilişkilidir? Bu makale ( 1006.1696 ) bu konuda ilgi çekici olabilir (özellikle ilk sayfanın ikinci sütununun son kısmı).
—
glS