Değişkenlerin pozitif veya negatif olmadığı varsayılarak, kenarın kenarları, verilerin sırasıyla 0 veya negatif olacağı noktalardır. Bu tür gerçek yaşam verileri doğru eğilme eğilimi gösterdiğinden, dağılımlarının alt ucunda daha fazla nokta yoğunluğu ve dolayısıyla kamanın "noktasında" daha fazla yoğunluk görürüz.
Daha genel olarak, PCA basitçe verilerin döndürülmesidir ve bu veriler üzerindeki kısıtlamalar, temel bileşenlerde genellikle soruda gösterildiği gibi görünecektir.
Aşağıda, günlük olarak normal dağıtılmış değişkenlerin kullanıldığı bir örnek verilmiştir:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

İlk iki bilgisayarın ima ettiği dönüşe bağlı olarak, kama görebilir veya biraz farklı bir sürüm görebilirsiniz, burada ( ordirgl()yerine plot()) kullanarak 3d olarak gösterin

Burada, 3B'de merkez kütleden dışarı çıkan birden fazla sivri uç görüyoruz.
Her birinin aynı ortalamaya ve varyansa sahip olduğu Gauss rastgele değişkenleri ( için bir nokta küresi görüyoruzXben∼ ( N) ( μ = 0 , σ= 1 )
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


Düzgün pozitif rastgele değişkenler için bir küp görüyoruz
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Burada, çizim için sadece 3 rastgele değişken kullanarak üniformayı gösterdiğimi ve böylece noktaların bir küpü 3d olarak tanımladığını unutmayın. Daha yüksek boyutlar / daha fazla değişkenle, 5d hiperküpü mükemmel bir şekilde 3D olarak temsil edemeyiz ve bu nedenle farklı "küp" şekli biraz bozulur. Benzer sorunlar gösterilen diğer örnekleri etkiler, ancak bu örneklerde kısıtlamaları görmek hala kolaydır.
Verileriniz için, PCA'dan önce değişkenlerin bir günlük dönüşümü, doğrusal bir regresyonda böyle bir dönüşümü kullanabileceğiniz gibi, kuyrukları çeker ve kümelenmiş verileri uzatır.
PCA grafiklerinde diğer şekiller de kırılabilir; böyle bir şekil, PCA'da korunan metrik gösterimin bir artefaktıdır ve at nalı olarak bilinir . Uzun veya baskın bir gradyanı olan veriler için (değişkenlerin 0'dan maksimuma çıktığı ve daha sonra verilerin bölümleri boyunca tekrar 0'a düştüğü tek bir boyut boyunca düzenlenmiş numunelerin bu tür artefaktlar ürettiği iyi bilinmektedir.
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

Eksenlerin uçlarındaki noktaların tekrar ortada büküldüğü aşırı bir at nalı üretir.

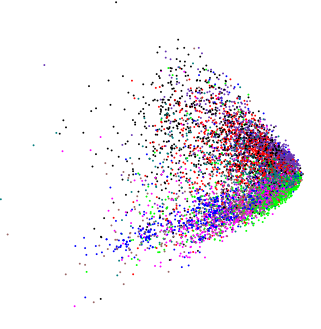 .
. (bu durumda gerçekten herhangi bir iç yapı olup olmadığını bilmek istedim).
(bu durumda gerçekten herhangi bir iç yapı olup olmadığını bilmek istedim).






