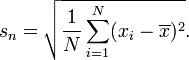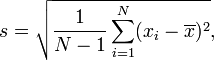ABD ve İngiltere Okulları Neden Standart Sapmayı Hesaplamanın Farklı Yöntemlerini Öğretiyor?

16

Anladığım kadarıyla Birleşik Krallık Okulları, Standart Sapmanın aşağıdakileri kullanarak bulunduğunu öğretir:

$alternatif metin$

ABD Okulları şunları öğretir:

$alternatif metin$

(yine de temel düzeyde).

Bu, geçmişte bazı öğrencilerimin İnternet'te arama yaptıkları, ancak yanlış bir açıklama buldukları için sorunlara neden oldu.

Neden fark var?

Basit veri kümeleri 10 değer söylüyorsa, yanlış yöntem uygulanırsa (örneğin bir sınavda) ne derece hata olur?

— Amos
kaynak

4

Birini ya da diğerini 'yanlış' formül olarak nitelendirmenin sorunu anlamanın yolu olup olmadığından emin değilim. Sadece ikincisinin, gerçek standart sapmanın tarafsız bir tahmincisi olması bakımından 'daha iyi' olmasıdır. Dolayısıyla, tarafsız tahminleri önemsiyorsanız, ikincisi 'daha iyi' / 'doğru' olur.

Formülü "yanlış" olarak nitelendiriyordum, eğer bir sınavda, müfredat tarafından yasaklanmamış formülü kullanırsanız, "yanlış" cevapla sonuçlanacaksınız demektir. Ayrıca, değerler kendi başına bir nüfus örneği değilse, ilk formül daha doğru bir değer verir.

— Amos

14

Srikant, ikincisinin tarafsız bir tahminci olduğunu düşünmüyorum. Bunun kare olan gerçek varyans yansız tahmin. Bununla birlikte, Jensen Eşitsizliği, rastgele değişkenin eğrisel bir fonksiyonunun beklentisinin, rastgele değişkenin beklentisinin fonksiyonu ile aynı olmadığını ortaya koymaktadır. Dolayısıyla, ikinci formül gerçek standart sapmanın tarafsız bir tahmincisi olamaz.

— Andrew Robinson

Çapraz referans için: @ m.SE ... de istendi

— JM, istatistikçi değil

4

Freedman, Pisani & Purves'ten tarafından çok popüler temel metin kullanarak herhangi bir ABD okul birinci formülü (kullanıyor

bir Amerikan İngiltere'de vs fark olarak bu nitelemek yanlıştır görünüyor böylece,).

s_{n}

$s_n$

— whuber

18

İlk formül popülasyon standart sapmasıdır ve ikinci formül ise örnek standart sapmasıdır. İkinci formül ayrıca varyansın tarafsız tahmincisi ile de ilgilidir - daha fazla ayrıntı için wikipedia'ya bakın.

Sanırım (burada) lisede örneklem ve nüfus arasında ayrım yapmıyorlar. Önyargılı tahmin ediciler gibi kavramlara kesinlikle dokunmazlar.

— csgillespie
kaynak

4

Standart sapmanın tarafsız bir tahmincisi olan Colin, genel durumda kapalı bir form temsiline sahip değildir. Var olan, varyansın (bu durumda s 2 ) tarafsız bir tahmincisidir. Her ikisinin de popülasyon varyansının tutarlı tahmin edicileri olduğu dikkate değerdir - ve böylece sürekli haritalama teoremi ile standart sapmaların iki tahmincisidir. İlgili bir nokta, s n 2 'nin s 2 ' den daha düşük bir MSE'ye sahip olmasıdır. Tarafsızlık empoze etmenin ek avantajı tartışmalıdır.

— mornington

@Tirthankar - çok özensiz. Cevabı biraz değiştirdim. Teşekkürler.

— csgillespie

2

Hatırladığım kadarıyla, GCSE matematik ve biliminde (14-16 yaş) 'örnek' hesaplaması öğretildi ve popülasyonlar ve örnekler ile bunlara ilişkin varyans ölçüleri arasındaki fark (derinlemesine olmasa da) A düzeyinde ( 16-18 yaş). Bu yüzden bunun basit bir İngiltere / ABD farkı olduğundan emin değilim.

— Freya Harrison

11

Çünkü henüz kimse son soruyu - yani iki formül arasındaki farkları ölçmek için bununla ilgilenelim.

Birçok nedenden dolayı, standart sapmaları farklılıklarından ziyade oranları açısından karşılaştırmak uygundur . Oran

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

$|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ İki veri kümesinin formalarını karşılaştırırken olduğu gibi SD'ler. (Veri kümeleri dengede olduğunda, tutarsızlıklar etkili bir şekilde tamamen ortadan kalkar ve her iki formül de aynı sonuçlara yol açar.) Muhtemelen, bunlar başlangıç öğrencilerine öğretmeye çalıştığımız akıl yürütme biçimleridir, bu yüzden öğrenciler hangi formülü kullanacakları konusunda endişe duyuyorlarsa, bu, metnin veya sınıfın gerçekten önemli olan şeyi vurgulamadığını gösteren bir işaret olarak alınabilir.

$N$ $t$ $z$ $s$ $s_n$

— whuber
kaynak

6

Bu Bessel'in Düzeltmesi . ABD versiyonu, örnek İngiltere sapmasının formülünü gösterir; burada yukarıdaki İngiltere versiyonu , numunenin standart sapmasıdır .

— Reed Copsey
kaynak

5

Bunun tamamen ABD ve İngiliz meselesi olduğundan emin değilim. Bu sayfanın geri kalanı yazdığım bir SSS'den alıntılandı. Http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Payda n-1 ile SD nasıl hesaplanır

Her değer ve örnek ortalama arasındaki farkın karesini hesaplayın.
Bu değerleri toplayın.
Toplamı n-1'e bölün. Sonuç varyans olarak adlandırılır.
Standart Sapmayı elde etmek için karekök alın.

Neden n-1?

Standart sapmayı hesaplarken neden n yerine n-1'e bölelim? 1. adımda, her bir değer ile bu değerlerin ortalaması arasındaki farkı hesaplarsınız. Nüfusun gerçek ortalamasını bilmiyorsunuz; tüm bildiğiniz örnek ortalamasıdır. Örnek ortalamasının popülasyon ortalamasına eşit olduğu nadir durumlar haricinde, veriler örnek ortalamasına gerçek popülasyon ortalamasından daha yakın olacaktır. Dolayısıyla, 2. adımda hesapladığınız değer, muhtemelen 1. adımda gerçek nüfus ortalamasını kullandığınızdan biraz daha küçük (ve daha büyük olamaz) olacaktır. Bunun için telafi etmek için n-1'e bölün buna nv denir Bessel düzeltmesi.

Peki neden n-1? Örnek ortalamasını ve değerlerden biri hariç hepsini biliyorsanız, son değerin ne olması gerektiğini hesaplayabilirsiniz. İstatistikçiler n-1 serbestlik derecesi olduğunu söylüyor.

SD ne zaman n-1 yerine n paydası ile hesaplanmalıdır?

İstatistik kitapları genellikle paydada biri n ve diğeri n-1 kullanarak SD'yi hesaplamak için iki denklem gösterir. Bazı hesap makinelerinde iki düğme bulunur.

N-1 denklemi, bir veri örneğini analiz ettiğiniz ve daha genel sonuçlar çıkarmak istediğiniz ortak durumda kullanılır. Bu şekilde hesaplanan SD (paydada n-1 ile), genel popülasyondaki SD değeri için en iyi tahmininizdir.

Sadece belirli bir veri kümesindeki varyasyonu ölçmek istiyorsanız ve daha geniş sonuçlara varmak için tahmin yapmayı planlamıyorsanız, paydadaki n'yi kullanarak SD'yi hesaplayabilirsiniz. Ortaya çıkan SD, bu belirli değerlerin SD'sidir. Bu noktaların çizildiği popülasyonun SD'sini tahmin etmek istiyorsanız, SD'yi bu şekilde hesaplamak mantıklı değildir. N'yi paydada sadece bir popülasyondan örnek alınmadığında, genel sonuçlar çıkarma arzusu olmadığında mantıklıdır.

Bilimin amacı neredeyse her zaman genellemektir, bu nedenle paydada n ile denklem kullanılmamalıdır. Nerede mantıklı olabileceğini düşünebileceğim tek örnek sınav puanları arasındaki değişimi ölçmek. Ancak çok daha iyi, her skorun bir dağılım grafiğini veya bir frekans dağılım histogramını göstermek olacaktır.

— Harvey Motulsky
kaynak

1

Öyle olduğunu söylemiyordum, sadece böyle bir farkın neden ortaya çıkabileceğini, yanlış tavsiyenin ardından ne tür bir hata verebileceğini ve öğrencilerime verebileceğim farkın iyi bir açıklaması olup olmadığını merak ediyordum. .

— Amos

@harvey - bağlantı öldü

— baxx

1

@baxx .. Bunu işaret ettiğiniz için teşekkürler. Sabit.

— Harvey Motulsky

3

N, veri kümesindeki nokta sayısı olduğu için, ortalamanın hesaplanmasıyla, veri kümesindeki özgürlük derecesini birer birer azalttığı iddia edilebilir (biri veri kümesine bağımlılık getirdiğinden), N Daha önce ortalamayı tahmin etmek zorunda olduğu bir veri kümesinden standart sapmayı tahmin ederken -1.

— Benjamin Bannier
kaynak