Bayes teoremi neyle ilgili?

Bayes teoremiyle ilgili kavramlar, yani ana fikirler nelerdir ? Karmaşık matematiksel gösterimin herhangi bir türevini istemiyorum.

Bayes teoremi nispeten basit fakat belli koşullu olasılıkların hesaplanmasına izin veren olasılık teorisinin temel sonucudur. Koşullu olasılıklar, sadece bir olayın diğerinin olasılığı üzerindeki etkisini yansıtan olasılıklardır.

Basitçe söylemek gerekirse, en ünlü haliyle, yeni veri verilen bir hipotez olasılığının ( P (H | D) ; arka olasılık denir), aşağıdaki denkleme eşit olduğunu belirtir: hipotezi verilen gözlenen verinin olasılığı ( P (D | H) , koşullu olasılık olarak adlandırılır), teorinin yeni kanıtlardan önce doğru olma olasılığını katlar ( P (H) , H'nin önceki olasılığını denir), bu verileri görme olasılığına bölünür; P (D ), D ) 'nin marjinal olasılığı olarak adlandırılır.

Resmen, denklem şöyle görünür:

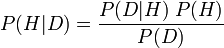
Bayes teoreminin önemi büyük ölçüde, kullanımın olasılıkla ilgili düşünce okulları arasındaki bir çekişme noktası olmasından kaynaklanmaktadır. Sübjektif bir Bayesçiye (olasılığı öznel inanç derecesi olarak yorumlayan) Bayes teoremi, öznel olasılık yargılarını denklem içine sokarak ve onunla birlikte çalıştırarak teori testi, teori seçimi ve diğer uygulamalar için temel taşı sağlar. Sıklıkla (olasılığı göreceli frekansları sınırlayan olarak yorumlayan ), Bayes teoreminin bu kullanımı bir kötüye kullanımdır ve bunun yerine anlamlı (öznel olmayan) öncelikler kullanmaya çalışırlar (nesnel Bayezanlar, olasılıkla başka bir olasılık yorumu altında).

Üzgünüm, burada bazı karışıklıklar var gibi görünüyor: Bayes teoremi, yaklaşmakta olan Bayesian- Frequentist tartışmasının tartışılması için yeterli değil. Her iki düşünce okuluyla da uyumlu bir teoremdir (Kolmogorov'un olasılık aksiyomları ile tutarlı olduğu düşünülürse).

Elbette, Bayes'in teoremi, Bayesian istatistiklerinin özüdür, ancak teorinin kendisi evrenseldir. Frekansistler ve Bayesanlar arasındaki çatışma, çoğunlukla, önceki dağılımların nasıl tanımlanıp tanımlanamayacağı ile ilgilidir.

Öyleyse, eğer soru Bayes teoremiyle ilgiliyse (ve Bayesian istatistikleri değil):

Bayes teoremi, belirli koşullu olasılıkları nasıl hesaplayabileceğini tanımlar. Örneğin, bildiğinizi düşünün: A semptomu olan birinin, hastalığı X p (A | X) olduğu göz önüne alındığında; genel olarak birinin X hastalığı (X) hastalığına sahip olma olasılığı; Birinin genel olarak semptomu olan A p (A) olasılığı. Bu 3 bilgi bilgisiyle, X hastalığına sahip birinin A semptomu olduğu göz önüne alındığında, X hastalığına sahip olma olasılığını hesaplayabilirsiniz.

Bayes teoremi, koşullu bir olasılık yi başka bir koşullu olasılık ' ya döndürmenin bir yoludur .$P(A|B)$$P(B|A)$

Bazıları için tökezleyen bir blok nın anlamıdır . Bu, yalnızca kesinlikle gerçekleştiği (veya doğru) olayları dikkate alarak olası olayların alanını azaltmanın bir yoludur . Mesela atılmış, adil, zarların altı, gösteren bir toprağa düşme olasılığı 1/6, ancak bir zarın altı sayıya düşmesi ihtimalinin düşmesi, , 1/3.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

Bayes teoremini kendiniz aşağıdaki gibi türetebilirsiniz. Koşullu bir olasılık oran tanımı ile başlayın:

$P(B|A) = \frac{P(AB)}{P(A)}$

burada ortak olasılığıdır ve ve marjinal olasılığıdır .$P(AB)$$A$$B$$P(A)$$A$

Şu anda formül gönderme , bu yüzden şunu da yazalım:$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

Bu işi yapmak için küçük bir hile yı görmek (Boole cebri tüm bunların altında olduğu için, göstererek bunu bir doğruluk tablosu ile kolayca kanıtlayabilirsiniz ), böylece yazabiliriz. :$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

Şimdi bunu formülüne yerleştirmek için yukarıdaki formülü tekrar yazınız, böylece solda kalır :$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

ve hey presto:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

Bu şekilde koşullu bir olasılığı döndürmenin ne anlama geldiğine gelince, birisinin bir semptom olması nedeniyle verilen bir hastalığa sahip olma olasılığını ortaya çıkarmaya çalışmanın ortak örneğini düşünün, yani bir semptom olduğunu biliyoruz - bunu gör - ama bir hastalıkları olup olmadıklarından ve onu sonuçlandırmak zorunda olmalarından emin olamayız. Ben formülle başlayacağım ve geri çalışacağım.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

Bu yüzden, bunu çözmek için, semptomun önceki olasılığını, hastalığın önceki olasılığını (yani, semptom ve hastalığın ne kadar yaygın veya nadir olduğunu) ve ayrıca birinin bir semptom olduğunu, birinin birisine tanıdığını verdiğimizi bilmeniz gerekir. bir hastalık (örneğin pahalı zaman alan laboratuar testleri ile).

Bundan çok daha karmaşık hale gelebilir, örneğin, birden fazla hastalığınız ve semptomunuz varsa, ancak fikir aynıdır. Daha genel olarak, Bayes teoremi genellikle nedenler (örn. Hastalıklar) ve etkiler (örneğin semptomlar) arasındaki ilişkilerin teorisine sahipseniz ve geriye doğru bir sebepten dolayı (örneğin, istediğiniz bazı semptomları görürseniz) ortaya çıkar. altta yatan hastalığın çıkarılması için).

İki ana düşünce okulu vardır İstatistik: sık ve Bayes .

Bayes teoremi ikincisi ile ilgilidir ve bir teorinin gerçek olma olasılığının yeni bir delilden nasıl etkilendiğini anlamanın bir yolu olarak görülebilir. Bu koşullu olasılık olarak bilinir. Sen bakmak isteyebilirsiniz bu matematik ele almak için.

Size çok sezgisel bir içgörü vereyim. Diyelim ki 10 kez yazı tura aldınız ve 8 kafa ve 2 yazı alacaksınız. Aklınıza gelebilecek soru, bu madalyonun kafalara doğru eğimli olup olmadığıdır.

Şimdi, geleneksel tanımlara veya sık sık olasılık yaklaşımıyla giderseniz, madalyonun tarafsız olduğunu ve bunun istisnai bir durum olduğunu söyleyebilirsiniz. Bu nedenle, atıcıların yanında kafa alma ihtimalinin de% 50 olduğu sonucuna varacaksınız.

Ama bir Bayesian olduğunuzu varsayalım. Gerçekten çok fazla sayıda kafaya sahip olduğunuzdan madalyonun kafa tarafına doğru bir önyargısı olduğunu düşünürdünüz. Bu olası önyargıyı hesaplamak için yöntemler var. Onları hesaplar ve bir dahaki sefere bozuk para attığınızda, kesinlikle bir kafa çağırırsınız.

Öyleyse, Bayesçi olasılık, gözlemlediğiniz verilere dayanarak geliştirdiğiniz inançla ilgilidir. Umarım bu yeterince basitti.

Bayes teoremi iki fikirle ilgilidir: olasılık ve olasılık. Olasılık diyor ki: Bu model göz önüne alındığında, bunlar sonuçlar. Yani: Adil bir para verildiğinde, zamanın% 50'sini alacağım. Olabilirlik diyor ki: Bu sonuçlar göz önüne alındığında, model hakkında söyleyebileceğimiz şey budur. Öyleyse: 100 kez bozuk para atarsanız ve 88 kafa alırsanız (önceki bir örneği alıp daha aşırı hale getirmek için), o zaman adil para modelinin doğru olma olasılığı o kadar yüksek değildir.

Bayes teoremini göstermek için kullanılan standart örneklerden biri, bir hastalık için test etme fikridir: popülasyonun 10000'ünden birinin sahip olduğu bir hastalık için% 95 kesinlikte bir test alırsanız, şansınız ne kadar? hastalığın var mı?

Naif cevap% 95'tir, ancak bu 10000 kişiden 9999'unda yapılan testlerin% 5'inin yanlış bir pozitif vereceği sorusunu görmezden geliyor. Yani hastalığa yakalanma ihtimaliniz% 95'ten çok daha düşük.

Belirsiz ifadeyi kullanmam "şans nedir?" Kasıtlı. Olasılık / olabilirlik dilini kullanmak: Testin doğru olma olasılığı% 95'tir, fakat bilmek istediğin şey hastalığın gerçekleşme olasılığıdır.

Biraz da konu dışı: Bayes teoreminin tüm ders kitaplarında çözmek için kullandığı diğer klasik örnek ise Monty Hall problemidir: Bir sınav programındasınız. Üç kapının birinin arkasında bir ödül var. Birinci kapıyı seçtin. Ev sahibi ödülü açığa çıkarmak için üçüncü kapıyı açar. İkinci şansı değiştirmeli misiniz?

Sorunun yeniden değerlendirilmesini seviyorum (aşağıdaki referansın izniyle): bir sınav programındasınız. Bir milyon kapıdan birinin arkasında bir ödül var. Birinci kapıyı seçtin. Ev sahibi ödülü açığa çıkarmak için 104632 kapısı dışındaki diğer bütün kapıları açar. 104632 numaralı kapıya mı geçmelisin?

Bayes teoremini, Bayes bakış açısıyla çok tartışan en sevdiğim kitap, David JC MacKay'ın "Bilgi Teorisi, Çıkarım ve Öğrenme Algoritmaları" dır. Bu bir Cambridge University Press kitabı, ISBN-13: 9780521642989. Cevabım (umarım) kitapta yapılan tartışmaların bir damıtmasıdır. (Genel kurallar geçerlidir: Yazarla hiçbir bağlantım yok, tıpkı kitabı seviyorum).

Bayes teoremi en belirgin haliyle, iki şeyin yeniden ifade edilmesidir:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

Yani simetriyi kullanarak:

$P(D|I) \neq 0$$P(D|I)$

Demek bu? Nasıl bu kadar basit bir şey bu kadar harika olabilir? Çoğu şeyde olduğu gibi, "hedefinden daha önemli olan yolculuk". Bayes teoremi buna yol açan argümanlardan dolayı kayalar.

$P(H|I)=1-P(\overline{H}|I)$

Şimdi tümdengelim mantığındaki "kural", "A'nın B'yi ima ettiği" bir ilişkiniz varsa, aynı zamanda "B'nin Not Yok" anlamına gelmesidir. Dolayısıyla "tutarlı bir muhakeme Bayes teoremini ima ediyor". Bu, "Bayes Değil teoremi, tutarlı bir muhakeme değil" anlamına gelir. yani, sonucunuz bir önceki ve olasılık için bir Bayesian sonucuna eşdeğer değilse, o zaman tutarsızca muhakeme yaparsınız.

Bu sonuç Cox teoremi olarak adlandırılır ve 1940'larda "Muhtemel çıkarım cebirinde" kanıtlanmıştır. Olasılık teorisinde daha yeni bir türev verilmiştir: Bilim mantığı.

Kevin Murphy'nin Bayes Teoremi'ne girmesini gerçekten çok seviyorum. Http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

Buradaki alıntı ekonomist bir makaleden alınmıştır:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

Bayesian yaklaşımının özü, yeni kanıtlar ışığında var olan inançlarınızı nasıl değiştirmeniz gerektiğini açıklayan matematiksel bir kural sağlamaktır. Başka bir deyişle, bilim adamlarının yeni verileri mevcut bilgileri veya uzmanlıklarıyla birleştirmelerini sağlar. Kanonik örnek, erken doğmuş bir yenidoğanın ilk gün batımını gözlemlediğini ve güneşin tekrar doğup kalkmayacağını merak ettiğini düşünmektir. Her iki olası sonucu da eşit öncelik olasılıkları atar ve bunu bir beyaz ve bir siyah mermerin bir torbaya yerleştirilmesiyle temsil eder. Ertesi gün, güneş doğduğunda, çocuk çantaya bir başka beyaz mermer koyar. Çantadan rastgele toplanan bir mermerin beyaz olma olasılığı (yani çocuğun gelecekteki güneş ışınlarına olan inanç derecesi) bu nedenle yarıdan üçte ikisine gitti. Güneş doğduktan sonra ertesi gün, Çocuk başka bir beyaz mermer ekler ve olasılık (ve bu nedenle inanç derecesinin) üçte ikisinden üçte birine kadar gider. Ve bunun gibi. Yavaş yavaş, her sabah güneşin doğmayacak kadar muhtemel olduğuna dair ilk inanç, güneşin daima yükseleceği kesinliğine yakın olacak şekilde değiştirildi.