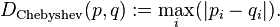Mesafe fonksiyonu nasıl optimize edilir?

Oldukça basit bir RTS benzeri oyun geliştirirken, mesafe hesaplamalarımın performansta bir etkiye neden olduğunu fark ettim.

Her zaman, bir birimin hedefine uygun olup olmadığını, merminin hedefine ulaşıp ulaşmadığını, oyuncu bir toplama, genel çarpışma vb. İki nokta arasındaki mesafe çok kullanılır.

Sorum tam olarak bununla ilgili. Oyun geliştiricilerin normal kare (x * x + y * y) yaklaşımı dışındaki mesafeleri kontrol etmek için hangi alternatifleri kullandıklarını bilmek istiyorum.

Manhattan mesafelerinin ve kare uzaklık karşılaştırmalarının farkında olduğumu belirtmek isterim (sqrt darboğazını atlayarak). Başka herhangi bir şey?

TL; DR; Sorununuz mesafe fonksiyonunu yerine getirmekten ibaret değil. Sorununuz mesafe fonksiyonunu birçok kez gerçekleştiriyor. Başka bir deyişle, matematiksel değil, algoritmik bir optimizasyona ihtiyacınız var.

[EDIT] Cevabımın ilk bölümünü siliyorum çünkü insanlar bundan nefret ediyor. Soru başlığı, düzenlemeden önce alternatif mesafe işlevlerini soruyordu.

Her zaman karekök hesapladığınız bir mesafe işlevi kullanıyorsunuz. Bununla birlikte, bunu sadece karekök kullanmadan değiştirebilir ve bunun yerine kare kareyi hesaplayabilirsiniz. Bu size çok değerli döngüleri kurtaracak.

Mesafe ^ 2 = x * x + y * y;

Bu aslında ortak bir hiledir. Ancak hesaplamalarınızı buna göre ayarlamanız gerekir. Gerçek mesafeyi hesaplamadan önce ilk kontrol olarak da kullanılabilir. Örneğin, bir kesişim testi için iki nokta / küre arasındaki gerçek mesafeyi hesaplamak yerine, Mesafe Karesini hesaplayabilir ve yarıçap yerine yarıçap kare ile karşılaştırabiliriz.

Düzenleme, @ Byte56'dan hemen sonra soruyu okumadığımı ve kare mesafe optimizasyonunun farkında olduğunuzu belirtti.

Sizin durumunuzda, maalesef neredeyse sadece Öklid Uzayıyla uğraşan bilgisayar grafiğindeyiz ve mesafe tam olarak Sqrt of Vector dot itselföklid uzayındaki gibi tanımlanıyor .

Mesafe karesi alacağınız en iyi yaklaşımdır (performans açısından), 2 çarpma, bir ekleme ve ödev veren hiçbir şey göremiyorum.

Yani mesafe fonksiyonunu optimize edemediğimi söylüyorsunuz ne yapmalıyım?

Sorununuz mesafe fonksiyonunu yerine getirmekten ibaret değil. Sorununuz mesafe fonksiyonunu birçok kez gerçekleştiriyor. Başka bir deyişle, matematiksel değil, algoritmik bir optimizasyona ihtiyacınız var.

Mesele, sahnedeki her nesneyle her karenin oyuncu kesişimini kontrol etmek yerine. Mekansal tutarlılığı kendi avantajınıza kolayca kullanabilirsiniz ve sadece oyuncunun yakınında bulunan nesneleri kontrol edebilirsiniz (en çok vurması / kesişmesi muhtemeldir).

Bu, bu uzamsal bilgiyi bir uzamsal bölümleme veri yapısında depolamak suretiyle kolaylıkla yapılabilir . Basit bir oyun için bir Izgara öneririm, çünkü temel olarak dinamik sahneyi güzelce uygulamak ve uygulamak kolaydır.

Her hücre / kutu, kılavuzun sınırlayıcı kutusunun içine aldığı nesnenin bir listesini içerir. Ve bu hücrelerdeki oyuncu pozisyonunu izlemek kolaydır. Mesafe hesaplamaları için, oyuncu mesafesini yalnızca sahnedeki her şey yerine, aynı veya komşu hücrelerin içindeki nesnelerle kontrol edin.

Daha karmaşık bir yaklaşım BSP veya Octrees kullanmaktır.

Herhangi bir mesafe boyunca doğrusal olarak kalan (aksine değil distance^2) ve yine de belirsiz biçimde dairesel görünen bir şeye ihtiyacınız varsa (squarish Chebyshev ve elmas benzeri Manhattan mesafelerinin aksine), sekizgen şeklindeki bir mesafe yaklaşımını elde etmek için son iki tekniği ortalayabilirsiniz:

dx = abs(x1 - x0)
dy = abs(y1 - y0)

dist = 0.5 * (dx + dy + max(dx, dy))

Wolfram Alpha sayesinde işte fonksiyonun bir görselleştirmesi (dağılım grafiği) :

Ve burada öklid mesafesine kıyasla hata fonksiyonunun bir grafiği (radyan, sadece ilk kadran):

Gördüğünüz gibi, hata eksenlerdeki% 0'dan loblarda yaklaşık% + 12'ye kadar değişmektedir. Katsayıları biraz değiştirerek onu +/-% 4'e indirebiliriz:

dist = 0.4 * (dx + dy) + 0.56 * max(dx, dy)

Güncelleştirme

Yukarıdaki katsayıları kullanarak, maksimum hata% +/- 4 arasında olacak, ancak ortalama hata% + 1,3 olacak. Sıfır ortalama hata için optimize edilmiş, şunları kullanabilirsiniz:

dist = 0.394 * (dx + dy) + 0.554 * max(dx, dy)

% -5 ile% + 3 arasında hata verir ve ortalama% + 0.043 hata verir.

Web'i bu algoritma için bir ad ararken, bu benzer sekizgen yaklaşımı buldum :

dist = 1007/1024 * max(dx, dy) + 441/1024 * min(dx, dy)

Bunun esasen eşdeğer olduğuna dikkat edin (üsler farklı olsa da - bunlar% -1,5 ila% 7,5 hata veriyor, ancak% +/- 4'e masaj yapılabilir) çünkü max(dx, dy) + min(dx, dy) == dx + dy. Bu formu kullanarak, minve maxçağrıları aşağıdakiler lehine kabul edilebilir:

if (dy > dx)
    swap(dx, dy)

dist = 1007/1024 * dx + 441/1024 * dy

Bu benim sürümümden daha mı hızlı olacak? Kim bilir ... derleyiciye ve hedef platform için her birini nasıl optimize ettiğine bağlıdır. Benim tahminimde herhangi bir fark görmek oldukça zor.

Bazen bu soru, mesafe hesaplamalarının gerçekleştirilmesinin maliyeti nedeniyle değil, hesaplamanın yapıldığı sayı nedeniyle ortaya çıkabilir .

Bir de büyük olan oyun dünyasında birçok aktör, öyle tırmanılamaz bir oyuncu ve tüm diğerleri arasındaki mesafeyi kontrol etmek. Daha fazla oyuncu, NPC ve mermiler dünyasına girmek üzere, ihtiyaç karşılaştırmalar sayısı artacak yapılacak quadratically ile O(N^2).

Bu büyümeyi azaltmanın bir yolu, istenmeyen aktörleri hesaplamalardan hızlıca silmek için iyi bir veri yapısı kullanmaktır.

Biz verimli yinelerler tüm aktörler için bir yol arıyoruz olabilir iken, aralığında olması çoğunluğu hariç olan aktörlerin dışı aralığında kesinlikle .

Eğer oyuncularınız dünyaya eşit bir şekilde yayılmışsa, bir kova ızgarası uygun bir yapı olmalıdır (kabul edilen cevabın önerdiği gibi). Aktörlere atıfları kaba bir ızgarada tutarak, kalanları göz ardı ederek menzil içinde olabilecek tüm aktörleri kapsamak için sadece yakındaki birkaç kovayı kontrol etmeniz yeterlidir. Bir aktör hareket ettiğinde, onu eski kovasından yenisine götürmeniz gerekebilir.

Daha az eşit şekilde yayılmış olan oyuncular için bir dörtlü , iki boyutlu bir dünya için daha iyisini yapabilir veya bir sekizli , üç boyutlu bir dünya için uygun olur. Bunlar, geniş boş alan alanlarını ve çok sayıda oyuncu içeren küçük alanları etkin bir şekilde bölümlendirebilen daha genel amaçlı yapılardır. İçin statik aktörler vardır ikili uzay bölümleme arama ama gerçek zamanlı olarak güncelleme için çok masraflı için çok hızlı (BSP). BSP'ler, tekrar tekrar yarıya kesmek için düzlemleri kullanarak alanı ayırır ve herhangi bir sayıda boyuta uygulanabilir.

Tabii ki, oyuncularınızı böyle bir yapıyı korumak için, özellikle de bölümler arasında hareket ederken, genel giderler var. Fakat birçok aktörün olduğu ancak küçük ilgi alanlarının olduğu büyük bir dünyada, maliyetlerin tüm nesnelere karşı saf bir şekilde karşılaştırmanın neden olduğu maliyetlerden çok daha düşük olması gerekir.

Bir algoritmanın giderinin, daha fazla veri alırken nasıl büyüdüğünü göz önünde bulundurmak, ölçeklenebilir yazılım tasarımı için çok önemlidir. Bazen sadece doğru veri yapısını seçmek yeterlidir. Maliyetler genellikle Big O notasyonu kullanılarak tanımlanır .

(Bunun sorunun doğrudan bir cevabı olmadığını biliyorum, ancak bazı okuyucular için faydalı olabilir. Vaktinizi boşa harcarsam özür dilerim!)

Chebyshev mesafesi ne durumda? P, q noktaları için şu şekilde tanımlanmıştır:

Böylece, (2, 4) ve (8, 5) puanları için, Chebyshev mesafesi 6'dır, | 2-8 | > | 4-5 |.

Dahası, E Euclid mesafesi ve C Chebyshev mesafesi olsun. Sonra:

Üst sınır muhtemelen kare kökü hesaplamanız gerektiğinden fazla kullanılmaz, ancak alt sınır yardımcı olabilir - Chebyshev mesafesi aralık dışında olacak kadar büyük olduğunda, Öklid mesafesi de sizi koruyabilir. hesaplamak zorunda kalmadan.

Elbette ki takas, Chebyshev mesafesinin menzil içindeyse, Euclid mesafesini yine de zaman harcayarak hesaplamanız gerektiğidir. Net bir kazanç olup olmadığını öğrenmenin tek yolu!

Çok basit bir yerel optimizasyon önce tek bir boyutu kontrol etmektir.

Yani :

distance ( x1, y1 , x1, y2) > fabs (x2 - x1)

Bu yüzden sadece fabs (x2 - x1)ilk filtre olarak kontrol etmek kayda değer bir kazanç sağlayabilir. Dünyanın büyüklüğüne ve ilgili aralığa ne kadar bağlı olacağı.

Ayrıca, bunu mekansal bölümleme veri yapısına bir alternatif olarak kullanabilirsiniz.

İlgili tüm nesneler bir listede x koordinat sırasına göre sıralanırsa, yakındaki nesnelerin listede yakın olması gerekir. Nesneler hareket ettikçe tam olarak korunmadıkları için liste düzensiz olsa bile, bilinen hız sınırları göz önüne alındığında, listedeki yakındaki nesneler için aranacak bölümü azaltabilirsiniz.

Geçmişte optimize etmek için çaba gösterildi sqrt. Artık bugünün makineleri için geçerli olmasa da, işte sihirli sayıyı kullanan Quake kaynak kodundan bir örnek 0x5f3759df:

float Q_rsqrt( float number )
{
  long i;
  float x2, y;
  const float threehalfs = 1.5F;

  x2 = number * 0.5F;
  y  = number;
  i  = * ( long * ) &y;  // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 ); // what the hell?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration (optional)
  // ...
  return y;
}

Bir ayrıntılı bir açıklama burada neler olup bittiğini Vikipedi'de bulunabilir.

Kısacası, makul bir ilk tahmin sağlamak için kullanılan sihir numarasıyla birlikte, Newton'un metodunun (yinelemeli olarak bir tahmin geliştiren sayısal bir algoritma) birkaç yinelemesidir .

Travis'in işaret ettiği gibi, bu tür bir optimizasyon artık modern mimarilerde kullanışlı değildir. Öyle olsa bile, sadece darboğazınıza hız kazandıran sabit bir hız sağlarken, algoritmik yeniden tasarım daha iyi sonuçlar alabilir.